The existence of closed forms on $M$ which are not differentials is related to the topological properties of $M$. One can show that every closed $k$-form on a vector space is the differential of some $k-1$ form. That is, every closed $k$-form in a vector space is exact.
Poincare's lemma for one forms
Let $\omega^1$ be a 1-form defined on $\R^n$, $n\geq 1$.
Then for $\phi(x) = \int_{x_0}^x \omega^1$ with $x_0\in \R^n$ and path $x_0\rightarrow x$ arbitrarily taken, we have the condition that
\begin{align*}
d\omega^0_{\phi}(\vec \xi) &= \lim_{\Delta t\rightarrow 0} \frac{\phi(\vec \xi\Delta t+\vec x_0)-\phi(\vec x_0)}{\Delta t}\\
&= \lim_{\Delta t\rightarrow 0} \frac{\int_{x_0}^{\xi\Delta t+x_0}\omega^1 - 0}{\Delta t}\\
&= \lim_{\Delta t\rightarrow 0} \frac{\omega^1 (\vec \xi\Delta t)}{\Delta t} \\
&= \omega^1(\vec \xi).
\end{align*}
Poincare's lemma for an arbitrary closed form
Proposition 1: In a vector space the integral of a closed form over any cycle is zero.
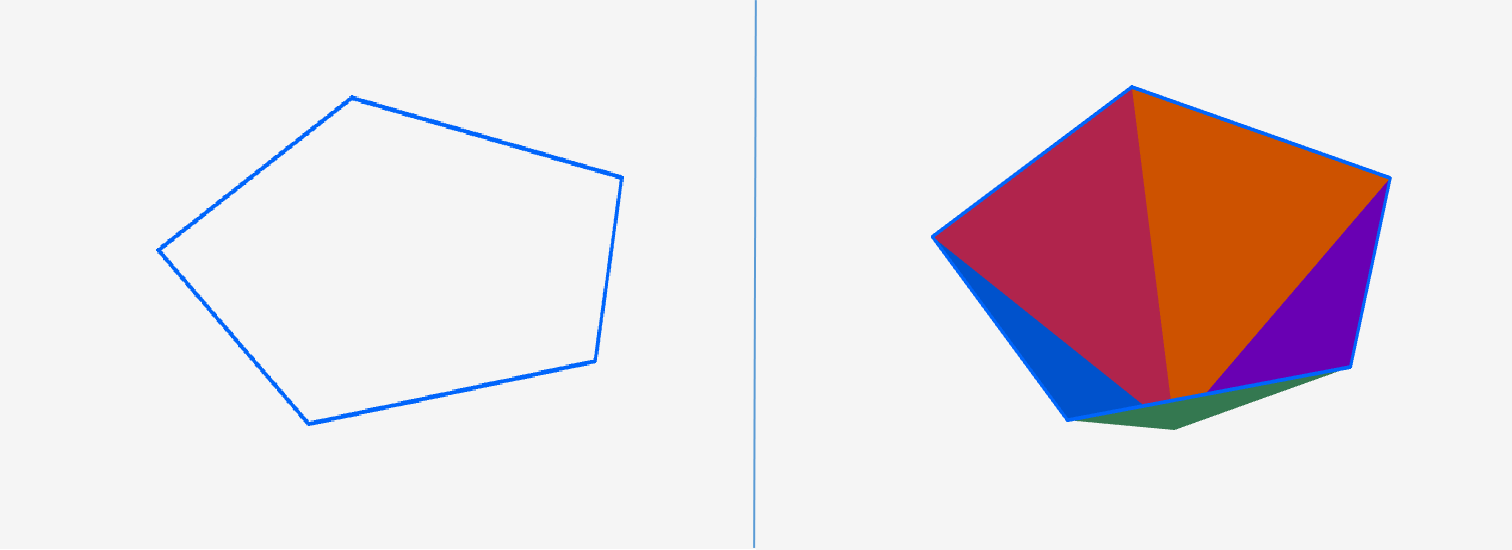
Proof: Let $c^m$ be a m-dimensional cycle in $\R^n$.
Construct cone $S=\{tc^m|t\in[0,1]\}$. This $S\subset \R^n$ because $\R^n$ is a convex set.
Suppose now $c^m = \sum_i \sigma_i$, then it's clear that
\begin{align*}
\partial c^m =\sum_i \partial \sigma_i= 0.\\
\end{align*}
From definition of $S$, we know that:
\begin{align*}
\partial S &= \partial \{tc^m|t\in[0,1]\}\\
&=\left\{\partial(t) \sum_i\sigma_i +t\sum_i-\partial \sigma_i|t\in[0,1]\right\}\\
&=\left\{(1)\sum_i \sigma_i\right\} \sqcup \left\{t\sum_i-\partial\sigma_i|t\in[0,1]\right\}\\
&=\sum_i \sigma_i
\end{align*}
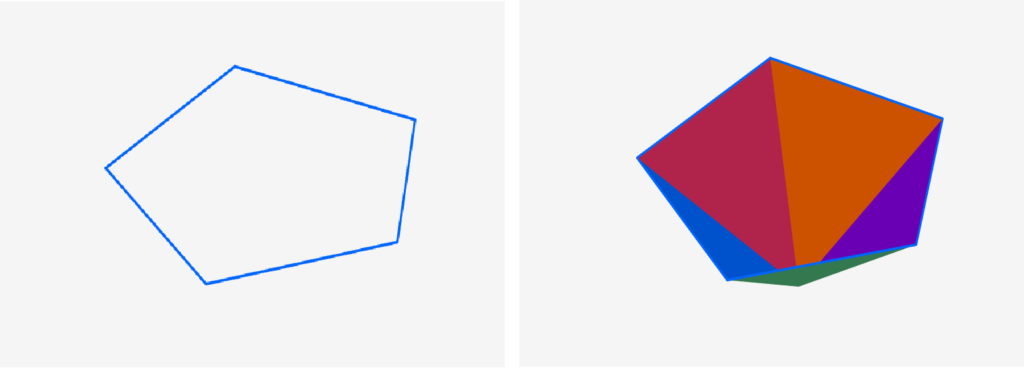
Thus we shall define cone operator $p: m$-cycle $ \rightarrow (m+1)$-chain in $\R^n$ given by:
$p(c^m) = \{tc^m|t\in[0,1]\}$, such that $\partial p(c^m) = c^m$.
Then we shall find that under Stoke's theorem,
$$\int_{c^k} \omega^k = \int_{pc^k} d\omega^k = 0 \text{ (since }\omega^k \text{ is closed)}.$$
$$\tag*{$\blacksquare$}$$
Proposition 2: For any $k$-chain $c$, $\partial(p c) + p(\partial c) = c$. That is, $\partial \circ p +p\circ\partial = 1$.
Proof:
Let $pc = S$, then again:
\begin{align*}
\partial S &= \partial \{tc|t\in[0,1]\}\\
&=\left\{(1)\sum_i \sigma_i\right\} \sqcup \left\{t\sum_i-\partial\sigma_i\bigg|t\in[0,1]\right\}\\
&=\sum_i \sigma_i -p\sum_i \partial\sigma_i\\
&=c-p(\partial c)
\end{align*}
Hence $p(\partial c)+\partial (pc) = c.$
$$\tag*{$\blacksquare$}$$
Proposition (Poincarè Lemma): Every closed form on a vector space is an exterior derivative.
Idea of the proof:
As we can observe from the 1D case, finding the form for which $d\Omega^{k-1} = \omega^k$ is somewhat similar to finding the "integral" of $\omega^k$. From the definition of exterior derivatives, we know that the condition that $\Omega^{k-1}$ must satisfy is that for any $k$-manifold $M$, $\int_M d\Omega^{k-1}=\int_M \omega^k$. Hence by Stoke's, this translates into that for any $k$-manifold $M$, $\int_{\partial M} \Omega^{k-1} = \int_M\omega^k$.
Now if it is the case that integral of $\omega$ over the "interior" of a manifold is equal to the integral of $\Omega$ over the boundary of a manifold, then we should intuitively think that the integral of $\Omega$ over any "segment" $s$ of the boundary must be equal to the integral of $\omega$ over the area that "segment" encloses. An tentative way of partioning the manifold is simply to find an arbitrary point inside $M$ which we call the "center" $c \in Int(M)$, and consider the enclosed area to be what is covered by radially "sweeping" the segment $s$ into the center $c$. Hence $\int_s \Omega = \int_{ps} \omega$.
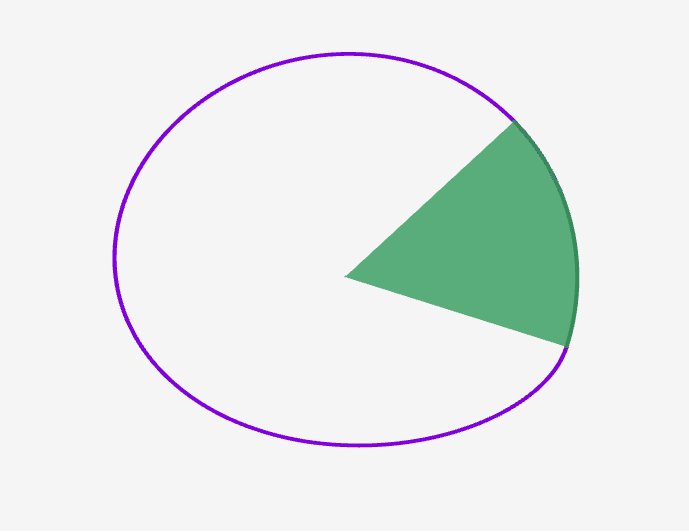
However, it must be the case that the choice of $c$ is non-unique. Because for any $c$ in the interior of $M$, we can define it to be the origin, hence $\int_{ps} \Omega$ would take on a different value. This is acceptable, as we can see in the case of integrals of 1-forms $\omega^1$, the resultant $\Omega^0$ can vary by a constant. Here the situation is analogous but with a catch. The point $c$ needs not lie in the manifold $M$, it can in fact be any point in space. Because the choice of $M$ can also be arbitrary with the same $\partial M$ as the boundary. For example, we can take $c_1 = (0,0,0)$ and $c_2 = (0,0.5,1)$. Then $\Omega$ can be validly defined to satisfy $\int_{s} \Omega = \int_{p_1 s}\omega$ or $\int_{s} \Omega = \int_{p_2 s}\omega$.
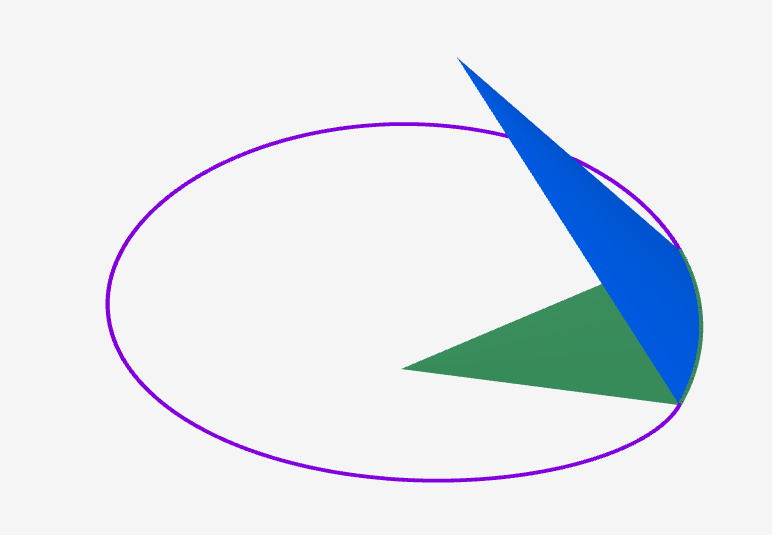
But in order for $\Omega$ to be well-defined, $\int_{\partial M} \Omega = \int_M \omega$ implies that for whichever choice of $M$ sharing the same boundary, $\int_M \omega$ must equate to the same value. This indeed would be the case if $\omega$ is a closed form: for k-manifolds $M_1$, $M_2$, if $\partial M_1 = \partial M_2$, then $M_1 - M_2$ have no boundaries,and $\int_{M_1-M_2} \omega = 0\Rightarrow \int_{M_1} \omega = \int_{M_2} \omega$ (by proposition 1). In particular, we shall ensure that $\int_{p_2 \partial M}\omega = \int_{p_1 \partial M}\omega$ for any choice of $p_1$, $p_2$ and $M$.

Proof:
We let $\omega$ be an arbitrary k-form on a vector space. We hope to show that it is exact by finding $\Omega$ s.t. $d\Omega = \omega$. To do so, we will need to define co-cone operator $p: \text{(k-1)-form}\rightarrow \text{k-form}$ s.t.:
$$\int_c p\omega = \int_{pc} \omega.$$
Construction of the co-cone operator:
Let the vector space be $V=R^n$. Let $\{\vec \xi_i|i \in [k-1]\}$ be $k-1$ vectors in $V$. Let $\Pi$ be a $k-1$ dimensional parallelogram s.t.
$$\Pi=\bigoplus_{i=1}^{k-1} \vec \xi_i.$$
We shall define differential form $\Omega$ by:
$$\Omega_{\vec x}(\Pi) = \lim_{\epsilon\rightarrow 0} \frac{\int_{p(\vec x+\epsilon^{k-1} \Pi)}\omega}{\epsilon^{k-1}}$$
$$\Rightarrow \lim_{\epsilon\rightarrow 0} \int_{p(\vec x+\epsilon^{k-1} \Pi)}\omega = \epsilon^{k-1} \Omega_{\vec x}^{k-1}(\Pi)+o(\epsilon^{k-1}).$$
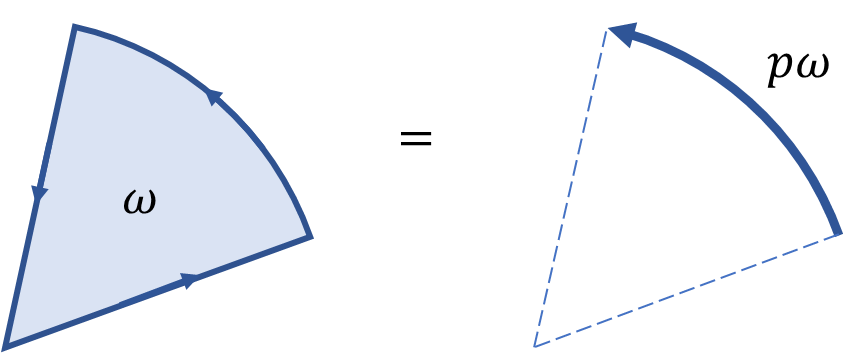
Now
\begin{align*}
\Omega_{\vec x}(\Pi) &= \lim_{\epsilon\rightarrow 0} \frac{\int_{p(\vec x+\epsilon^{k-1} \Pi)}\omega}{\epsilon^{k-1}}\\
& = \lim_{\epsilon\rightarrow 0} \frac{1}{\epsilon^{k-1}} \int_{[0,1]^k} \omega_{\vec x t+ \vec \xi_i s_i \epsilon t}(\vec x + \vec \xi_i s_i \epsilon, \epsilon t \vec \xi_1 ds_1, \epsilon t \vec \xi_2ds_2 ,..., \epsilon t \vec \xi_{k-1}ds_{k-1})dt\\
&= \lim_{\epsilon\rightarrow 0} \frac{1}{\epsilon^{k-1}} \int_{[0,1]^k} \omega_{\vec x t+ \vec \xi_i s_i \epsilon t}( \vec x, t \vec \xi_1, t \vec \xi_2 ,..., t \vec \xi_{k-1})\epsilon^{k-1} ds_1 ds_2 ... ds_{k-1} dt\\
&= \lim_{\epsilon\rightarrow 0} \frac{1}{\epsilon^{k-1}} \int_{[0,1]^k}( \vec x, \omega_{\vec x t}( t \vec \xi_1, t \vec \xi_2 ,..., t \vec \xi_{k-1})\epsilon^{k-1} + o(\epsilon^k-1)) ds_1 ds_2 ... ds_{k-1} dt\\
&= \lim_{\epsilon\rightarrow 0} \frac{1}{\epsilon^{k-1}} \int_0^1\omega_{\vec x t}(\vec x, t \vec \xi_1, t \vec \xi_2 ,..., t \vec \xi_{k-1})\epsilon^{k-1} dt\\
&=\int_0^1\omega_{\vec x t}(\vec x, \vec \xi_1, \vec \xi_2 ,..., \vec \xi_{k-1})t^{k-1}dt.\\
\end{align*}
Now obviously $\Omega$ is linear and hence a differential form, and additionally for any $(k-1)$-chain $c$, we have that:
\begin{align*}
\int_c \Omega &= \int_c \Omega(dc)\\
&=\int_c \int_{p(dc)}\omega\\
&=\int_{p(\int_cdc)}\omega\\
&=\int_{pc}\omega
\end{align*}
So if we let: $$(p\omega)_{\vec x}(\Pi) \equiv \Omega_{\vec x}(\Pi) = \int_0^1\omega_{\vec x t}( \vec \xi_1, \vec \xi_2 ,..., \vec \xi_{k-1}, \vec x)t^{k-1}dt,$$
then we obtain : $\int_c p\omega = \int_{pc} \omega$ and hence the definition of the co-cone operator.
Putting it together:
We now claim that for any closed form $\omega$, $p\omega$ is the "anti-differential". Check:
\begin{align*} \int_c d(p\omega) &= \int_{\partial c} p\omega\\
&= \int_{p\partial c} \omega \ \ \ \ \text{ (from definition of $p\omega$)} \\
&= \int_{c-\partial pc} \omega \ \ \ \ \text{ (from proposition 2)}\\
&= \int_{c} \omega-\int_{\partial pc} \omega.
\end{align*}
Since $\omega$ is a closed form, $\partial(pc)$ is a cycle, thus,
$$ \int_c d(p\omega) = \int_{c} \omega.$$
Because we can take $c$ to be arbitrary, $d(p\omega)=\omega$, and $\omega$ is exact.
$$\tag*{$\blacksquare$}$$