Introduction
Landau's textbook on Lagrangian mechanics is in the form of an A Priori, starting with the principle of least action as the founding stone of mechanical systems, which directly gives rise to the Lagrange-Euler equation $$\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}=\frac{\partial L}{\partial q}.$$ Such a direct approach cannot quite bring conviction to someone who begins with Newtonian mechanics. Some simplistic lines of deductions can produce Newton's third law based on the Euler-Lagrange equations, but it is limited to free moving particles that aren't constrained in any particular direction with cannonical coordinates. The validity behind Lagrange-Euler's equations become obscure when it comes to generalized coordinates, coordinates that aren't necessarily inertial or spanning the entire space. What I did is thus deriving from the Newtonian framework the exact terms of the Euler-Lagrange equations for generalized coordinates, while hoping to inspire some new understandings.
Internal work theorem
Internal work theorem states that the net work done by internal forces of a system over any virtual displacements always sum up to 0. We call the displacements virtual because sometimes the system isn't necessarily moving in that direction, but we can hypothesize the movement and observe that the energy must be conserved. This works because if the system indeed has the initial velocities that manifests the hypothesized displacements over a period of $dt$, the total kinetic energy shall not vary. Internal forces serve to balance out the acceleration of components in a system with constraints, and cannot be accounted for with potential energy or friction. Essentially, forces acting on particles in all systems that eventually attribute to their accelerations can be decomposed into internal and external forces. Mathematically the internal work theorem is expressed as
$$\sum_i^n\vec{F}_{iI} \cdot d\vec{r}_i=0,$$ where $\vec{F}_{iI}$ is the internal force acting on the $i$-th particle and $d\vec{r}_i$ denoting the differential (and hence linear) displacement of the particle under its constraint conditions. Sometimes if a system were to move in different directions the ratio of work over distance on its individual parts might differ and hence the force, but the internal work theorem shall stay true regardless.
Example - Torque
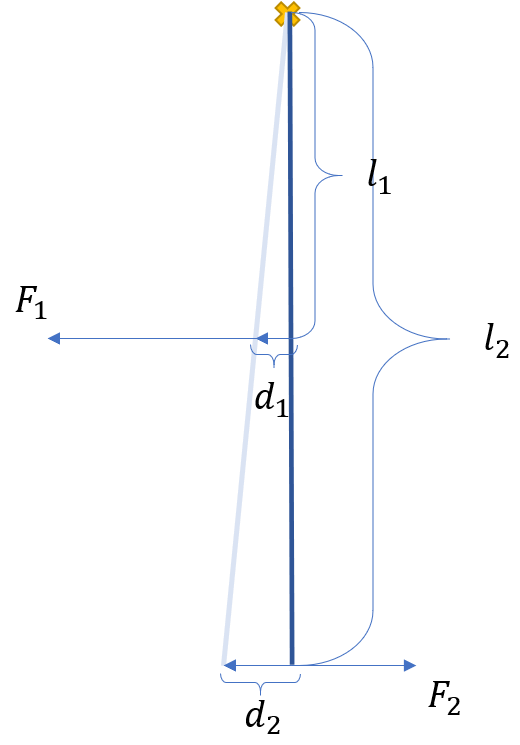
Lever principle, or otherwise generalized into torque, serves as a good example for the internal work theorem. It states that under equilibrium the driving force multiplied by the driving arm length is equal to the response force multiplied by the response arm length, i.e., $F_1l_1=F_2l_2$. Or, when there are multiple points on which normal forces are applied, $$\sum_i^n \tau_i=\sum_i^nl_iF_i=0,$$ namely the net torque have to cancel out under equilibrium. This is how energy flows internally under all situations inside the system, whether moving inertially or accelerated by external forces. Nothing in the four laws proposed by Newton stated what is to be expected when rotation is involved, but it is nevertheless a reliable fact that torque is the additive quantity under experiments.
This driving factor of motion called torque is one among the generalized forces. Generalized forces are not exactly forces, in that they don't have to encourage linear motion, it can be rotation, deformation, and so on. To understand it, we need to see it from the perspective of work and energy. In shortest terms, there is no way for internal forces to do any work, they only flow between different parts of the system. In the torque scenario, when we wish to increase $d_2$, $d_1$ has to move accordingly, and by geometry under the differentiation we know that $\frac{d_2}{d_1}=\frac{l_2}{l_1}$. Therefore upon moving the system we have input of energy $F_1\cdot d_1$, and output of energy $F_2\cdot d_2$, and the relation $F_1\cdot d_1+F_2\cdot d_2=0$ regardless the exact value of $d_1$ and $d_2$. While we don't know their exact values, their ratio can be known, and that is, given that $F_1$ and $F_2$ were already parallel to $d_1$ and $d_2$, $$F_1d_1+F_2d_2 = 0 \Rightarrow F_1l_1+F_2l_2 = 0.$$
Net work done on a system of $n$ particles
Now it's the time to take things up a notch. Suppose that with $m$ generalized coordinates, we can fully determine the position of $n$ particles at any time uniquely. We can, in theory, completely describe the instantaneous work done to a system of $n$ components with the distance travelled by its individual components $d\vec{r}_i$ and the force being exerted on these components $\vec{F}_i$ in this duration. And further, each coordinate $\vec{r}_i$ can be expressed in terms of the set of generalized coordinates $$\vec{r}_i=\vec{r}_i(q_1, q_2,…,q_m),$$ so that we not only know the motion of the individual particles, we also know how their movements are constrained together. This would give the total work in the integral form:
$$\begin{aligned} W&=\sum_i^n\int \vec{F}_i\cdot d\vec{r}_i\\&=\sum_i^n\int \vec{F}_i\cdot (\sum_j^m \frac{\partial\vec{r}_i}{\partial q_j}dq_j)\\&=\int\sum_i^n\sum_j^m\vec{F}_i\cdot \frac{\partial \vec{r}_i}{\partial q_j}dq_j \end{aligned}$$
We can now separate $\vec{F}_i$ acting on each component into the internal force $\vec{F}_{iI}$ and the external force $\vec{F}_{iE}$ acting on it: \begin{aligned} W&=\int\sum_i^n\sum_j^m(\vec{F}_{iI}+\vec{F}_{iE})\cdot \frac{\partial \vec{r}_i}{\partial q_j}dq_j\\ &=\int \sum_j^m(\sum_i^n\vec{F}_{iI}\cdot \frac{\partial \vec{r}_i}{\partial q_j}dq_j+\sum_i^n\vec{F}_{iE}\cdot \frac{\partial \vec{r}_i}{\partial q_j}dq_j), \end{aligned}
in which $\sum_i^n\vec{F}_{iI}\cdot \frac{\partial \vec{r}_i}{\partial q_j}dq_j$ cancels out to 0 due to the internal work theorem. Leaving us with $$W=\int \sum_j^m\sum_i^n\vec{F}_{iE}\cdot \frac{\partial \vec{r}_i}{\partial q_j}dq_j.$$ Then in a conservative force field with potential $U$, where $\vec{F_i}=\frac{\partial U}{\partial \vec{r}_i}$ $$\frac{\partial W}{\partial q_j}=\sum_i^n\vec{F}_{iE}\cdot\frac{\partial \vec{r}_i}{\partial q_j}=\sum_i^n\frac{\partial U}{\partial \vec{r}_i}\cdot \frac{\partial \vec{r}_i}{\partial q_j}=\frac{\partial U}{\partial q_j}.$$
Generalized Momentum
Kinetic energy describes the total work done to the system in terms of the momentum and velocity of its components. I think its only fair to argue that kinetic energy is also a relative quantity, just like potential energy or work, in that we cannot really say what the absolute kinetic energy of the system is, but only capable of knowing how it changes after work has been done. Of course, it's convenient to say that the kinetic energy is the work it takes to accelerate the entire system from static state to its current motion, in reality the "static state" really depends on the reference frame, and hence is an equally arbitrary measurement.
To derive kinetic energy of $n$ components, which is defined as the work needed to accelerate the system from its static state to its current motion, we have under cannonical coordinates:
\begin{aligned} T&=W\big| _0^V\\ &=\int_0^R\sum_i^n\vec{F_i}\cdot d\vec{r}_i=\int_0^T\sum_i^n\vec{F_i}\cdot \frac{d\vec{r}_i}{dt}dt\\ &=\int_0^T\sum_i^n\frac{d\vec{r}_i}{dt}\cdot\vec{F_i}dt=\int_0^T\sum_i^n\frac{d\vec{r}_i}{dt}\cdot d\vec{p}_i\\ &=\int_0^V\sum_i^n m_i\vec{v}_i\cdot d\vec{v}_i \end{aligned}
The generalized momentum is defined by $\frac{\partial T}{\partial \dot{q}_k}$, where $\dot{q}_k$ is the $k$-th generalized coordinate of the system. Then
$$\begin{aligned} \frac{\partial T}{\partial \dot{q}_k}&=\frac{\partial }{\partial \dot{q}_k}\int_0^V\sum_i^n m_i\vec{v}_i\cdot d\vec{v}_i\\ &=\frac{\partial}{\partial \dot{q}_k}\int_0^V\sum_i^n m_i(\sum_j^m\frac{\partial\vec{r}_i}{\partial q_j}\frac{dq_j}{dt})\cdot d(\sum_j^m\frac{\partial\vec{r}_i}{\partial q_j}\frac{dq_j}{dt})\\ &=\frac{\partial}{\partial\dot{q}_k}\int_0^V\sum_i^n m_i(\sum_j^m\frac{\partial\vec{r}_i}{\partial q_j}\frac{dq_j}{dt})\cdot \sum_j^m(\frac{\partial\vec{r}_i}{\partial q_j}d\dot{q}_j+\dot{q}_jd\frac{\partial\vec{r}_i}{\partial q_j}) \end{aligned}$$
Since $d\frac{\partial\vec{r}_i}{\partial q_j}$ describes the change in the ratio between increment of $q_j$ and increment of $\vec{r}_i$ is independent of the change in $\dot{q}$ and only dependent upon the change in $q$ (imagine a point moving in a skewed spatial coordinate system and see that the ratio between its canonical movement and its movement along a coordinate completely depends on the spatial position of the point regardless how fast it is traveling in non-relativistic scenarios), the partial differentiation yields:
$$\begin{aligned} \frac{\partial T}{\partial\dot{q}_k}&=\frac{\partial}{\partial \dot{q}_k}\int_0^V\sum_i^n m_i(\sum_j^m\frac{\partial\vec{r}_i}{\partial q_j}\frac{dq_j}{dt})\cdot \sum_j^m(\frac{\partial\vec{r}_i}{\partial q_j}d\dot{q}_j+\dot{q}_jd\frac{\partial vec{r}_i}{\partial q_j})\\ &=\sum_i^n m_i(\sum_j^m \frac{\partial r_i}{\partial q_j}\frac{dq_j}{dt})\cdot \frac{\partial\vec{r}_i}{\partial q_k}\\ &=\sum_i^n m_i\vec{v}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k} \end{aligned}$$
Now this is a very clean expression, from this we now know that the generalized momentum $\frac{\partial T}{\partial q_j}$ is exactly the sum of the momenta of all the system's components along the direction in which a variational change in $q_j$ causes. And the more $\vec{r}_i$ changes in accordance with a unit change of $q_j$ in that instant, the more generalized momentum along $q_j$ there is, which agrees with the internal work theorem.
Then the generalized force is equal to the time derivative of generalized momentum:
$$\begin{aligned}
\frac{d}{dt}\frac{\partial T}{\partial \dot{q}_k}=&\frac{d}{dt}\sum_i^n m_i\vec{v}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k}\\
=&\sum_i^n(m_i\frac{d}{dt}\vec{v}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k}+m_i\vec{v}_i\cdot\frac{d}{dt}\frac{\partial\vec{r}_i}{\partial q_k}).
\end{aligned}$$
Observe that the generalized force acting on the coordinate $q_k$ is composed of two parts --- the acceleration of the components along the motion of $q_k$ and the acceleration of the inertial space relative to $q_k$.
Since for mechanical systems the potential energy $U$ is independent of the velocity of any component of the system, we know $\frac{\partial L}{\partial\dot{q}_k} = \frac{\partial(T-U)}{\partial\dot{q}}=\frac{\partial T}{\partial\dot{q}}$, and hence $$\frac{d}{dt}\frac{\partial L}{\partial\dot{q}}=m_i\sum_i^n (\frac{d}{dt}\vec{v}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k}+\vec{v}_i\cdot\frac{d}{dt}\frac{\partial\vec{r}_i}{\partial q_k}).$$
$\frac{\partial L}{\partial q_k}$-the generalized force
$$\begin{aligned}\frac{\partial L}{\partial q_k}&=\frac{\partial T}{\partial q_k}-\frac{\partial U}{\partial q_k}\\&=\frac{\partial}{\partial q_k}\int_0^T\sum_i^n m_i(\sum_j^m\frac{\partial\vec{r}_i}{\partial q_j}\frac{dq_j}{dt})\cdot \sum_j^m(\frac{\partial\vec{r}_i}{\partial q_j}d\dot{q}_j+\dot{q}_jd\frac{\partial\vec{r}_i}{\partial q_j})+\sum_i^n\vec{F}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k}\\&=\sum_i^n \left(m_i \left(\sum_j^m\frac{\partial\vec{r}_i}{\partial q_j}\dot{q}_j\right)\cdot\left(\sum_j^m\dot{q}_j\frac{\partial}{\partial q_k}\frac{\partial\vec{r}_i}{\partial q_j}\right)\right)+\sum_i^n\vec{F}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k},\end{aligned}$$
in which $\sum_j^m\dot{q}_j\frac{\partial}{\partial q_k}\frac{\partial\vec{r}_i}{\partial q_j}$ is changes in $\frac{\partial\vec{r}_i}{\partial q_j}$ caused by the coordinate motion of $q_j$. And further by equivalence of the second order derivatives
$$\begin{aligned}\sum_j^m\dot{q}_j\frac{\partial}{\partial q_k}\frac{\partial\vec{r}_i}{\partial q_j}&=\sum_j^m\dot{q}_j\frac{\partial}{q_j}\frac{\partial\vec{r}_i}{\partial q_k}\\&=\sum_j^m\frac{\partial}{\partial q_j}\frac{\partial\vec{r}_i}{\partial q_k}\frac{dq_j}{dt}\\&=\frac{d}{dt}\frac{\partial\vec{r}_i}{\partial q_k}.\end{aligned}$$
Hence combined we have
$$\begin{aligned}\frac{\partial L}{\partial q_j}&=\sum_i^n \left(m_i \left(\sum_j^m\frac{\partial\vec{r}_i}{q_j}\dot{q}_j\right)\cdot\left(\sum_j^m\dot{q}_j\frac{\partial}{\partial q_k}\frac{\partial\vec{r}_i}{\partial q_j}\right)\right)+\sum_i^n\vec{F}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k}\\&=\sum_i^n \left(m_i \vec{v}_i\cdot\frac{d}{dt}\frac{\partial\vec{r}_i}{\partial q_k}\right)+\sum_i^n\vec{F}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k}\\&=\sum_i^n m_i \vec{v}_i\cdot\frac{d}{dt}\frac{\partial\vec{r}_i}{\partial q_k}+\sum_i^n m_i\frac{d}{dt}\vec{v}_i\cdot\frac{\partial\vec{r}_i}{\partial q_k}\\&=\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}\end{aligned}$$
System with non conservative force & Generalized Forces
But when there are non-conservative external forces that can't be accounted by potential, we write that as $\vec{F}_{ni}$, it must also be accounted into the acceleration of $\vec{a}_i$. Note that the term $m_i\vec{v}_i\cdot \frac{d}{dt}\frac{\partial\vec{r}_i}{q_k}$ is independent of the acceleration $\vec{a}_i$, is determined only by $\vec{v}_i$, and is cacnelled out by the same term in $\frac{\partial L}{\partial q_k}$, $\vec{F}_{ni}$ has no effect on this term.
To distinguish between conservative and non-conservative forces, we denote $\vec{F}_{ci}$ and $\vec{F}_{ni}$ to each.
Then we have
$$\begin{aligned}\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_k}-\frac{\partial L}{q_k}&=\sum_i^n(m_i\vec{a}_i\cdot \frac{\partial\vec{r}_i}{\partial q_k}+\dots)-\sum_i^n(\vec{F}_{ci}\cdot \frac{\partial\vec{r}_i}{\partial q_k}+\dots)\\&=\sum_i^n(m_i\vec{a}_i\cdot \frac{\partial\vec{r}_i}{\partial q_k}-\vec{F}_{ci}\cdot \frac{\partial\vec{r}_i}{\partial q_k})\\&=\sum_i^n(\vec{F}_{ni}\cdot\frac{\partial\vec{r}_i}{\partial q_k}).\end{aligned}$$
We call $$Q_k=\sum_i^n(\vec{F}_{ni}\cdot\frac{\partial\vec{r}_i}{q_k})$$ the generalized forces applied externally (outside the conservative system). Combined, $$\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_k}-\frac{\partial L}{\partial q_k}=Q_k$$