(Arnold Appendix 3, Cohomology & Homology, problem 15)
A rough outline of the proof will be to first identify a representation for the $T^2$ manifold, and then finding a representation of the set of closed forms and differential forms on $T^2$. Next we shall find an isomorphism that maps between the cohomology group $H^1(T^2, \R)$ and $\R^2$, by verifying that it is well-defined and bijective.
A two torus has structure $T^2 = S^1\times S^1$. We shall parameterize $S^1$ by $\phi\in [0, 2\pi) \rightarrow S^1$. Then $T^2$ is naturally parameterized by chart $(\phi_1, \phi_2)\in [0, 2\pi)^2 \rightarrow S^1 \times S^1$. Noting the space continues into $\phi = 0$ at $\phi = 2\pi$, we shall always impose continuity conditions between $\phi = 2\pi$ and $\phi = 0$ on analytical functions.
The set of closed forms $\omega^1$ on $T^2$ satisfy:
Suppose $a: T^2 \rightarrow \mathbb{R}$, $b: T^2 \rightarrow \mathbb{R}$, both analytic, then $\omega^1 = a d\phi_1+b d\phi_2$ defines an arbitrary 1-form on $T^2$ and:
$$\omega^1 \text{closed} \Rightarrow d\omega^1 = 0.$$
So by previous condition:
\begin{align*}d\omega^1 &= \frac{\partial a}{\partial \phi_2} d\phi_2 \wedge d\phi1 + \frac{\partial b}{\partial \phi_1} d\phi_1 \wedge d\phi2 \\ &= \left( \frac{\partial b}{\partial \phi_1} -\frac{\partial a}{\partial \phi_2}\right)d\phi_1 \wedge d\phi2 = 0.\\\Rightarrow &\frac{\partial b}{\partial \phi_1} = \pd{a}{\phi_2}.\end{align*}
Hence we shall represent the set of all closed 1-forms on $T^2$ by:
$$C=\{(a,b)|a,b:T^2\rightarrow \R, \partial_{\phi_2}a = \partial_{\phi_1} b\}.$$
(here we denote by $(a,b)$, $ad\phi_1 +b d\phi_2$)
The set of differential 1-forms on $T^2$ satisfy:
$\exists f:T^2\rightarrow \R$ analytic, such that
$$\omega^1 = df = \pd{f}{\phi_1} d\phi_1 + \pd{f}{\phi_2} d\phi_2.$$
So we shall represent the set of all differential 1-forms on $T^2$ by:
$$D=\{df|f:T^2\rightarrow \R\}.$$
(here we denote by $df$, $\partial_{\phi_1}fd\phi_1 +\partial_{\phi_2}f d\phi_2$).
Then the cohomology group $H^1(T^2, \R)$ is defined by
$$H^1(T^2, \R)= \frac{C}{D}.$$
Now we define $H:\frac{C}{D}\rightarrow \R^2$ given by:
$$H([(a,b)])=\left(\int_0^{2\pi}a(\phi_1,0)d\phi_1, \int_0^{2\pi}b(0,\phi_2)d\phi_2\right).$$
(we denote by $[(a,b)]$, the coset of $(a,b)$)
We claim that H is an isomorphism.
- $H$ is Well-defined. Let $(a',b')\in[(a,b)]$, then $\exists f\in D$, s.t. $(a',b') = (a+\partial\phi_1f, b+\partial\phi_2f)$.
\begin{align*}H((a'b'))&=\left(\int_0^{2\pi}(a+\partial_{\phi_1}f)(\phi_1,0)d\phi_1, \int_0^{2\pi}(b+\partial_{\phi_2}f)(0,\phi_2)d\phi_2\right)\\&=\left(\int_0^{2\pi}ad\phi_1+\int_0^{2\pi}\partial_{\phi_1}f(\phi_1,0)d\phi_1, \int_0^{2\pi}bd\phi_2+\int_0^{2\pi}\partial_{\phi_2}f(0,\phi_2)d\phi_2\right)\\&=\left(\int_0^{2\pi}ad\phi_1+f(\phi_1,0)\biggr|_0^{2\pi}, \int_0^{2\pi}bd\phi_2+f(0,\phi_2)\biggr|_0^{2\pi}\right)\end{align*}
By continuity condition, $f(\phi_1,0)\biggr|_0^{2\pi} = 0$ and $f(0,\phi_2)\biggr|_0^{2\pi} = 0$. Thus
$$H((a'b'))=\left(\int_0^{2\pi}ad\phi_1, \int_0^{2\pi}bd\phi_2\right)=H((a,b)).$$
Hence $H$ yields the same value for all elements of $[(a,b)]$.
- Injective:
Let $[(a,b)], [(a',b')] \in \frac{C}{D}$ such that $H[(a,b)] = H[(a',b')]$. i.e.
\begin{align*}&\int_0^{2\pi}a(\phi_1,0)d\phi_1\equiv\int_1a = \int_0^{2\pi}a'(\phi_1,0)d\phi_2 \equiv \int_1a'\\&\int_2b=\int_2b'.\end{align*}
Now because $\partial_2a = \partial_1b, \exists g:[0,2\pi]^2\rightarrow \R$ s.t. $a=\partial_1g, b=\partial_2g$. (consider double integral of $c=\partial_2a=\partial_1b$ over $[0,2\pi]^2$)
Likewise, $\exists g':[0,2\pi]^2\rightarrow\R$s.t.$a'=\partial_1g', b'=\partial_2g'$.
Now consider $f=g-g'$, we want to show that $f$ is $c^\infty$ on $T^2$. We already know that $f$ is analytical on the range $[0,2\pi]^2$, since both $g$ and $g'$ are analytical on this range. Then if $f$ goes back to itself on the boundaries of $[0,2\pi]^2$, namely that if $\forall \phi_1, f(\phi_1,0)=f(\phi_1, 2\pi)$ and that $\forall\phi_2, f(0,\phi_2) = f(2\pi, \phi_2)$, it will be $c^0$. And because $\partial_1f = a-a'$ and $\partial_2f =b-b'$, both are $c^\infty$, $f$ is consequently also $c^\infty$.
Now
\begin{align*}f(0, 2\pi)-f(0,0) &= \int_0^{2\pi}\partial_{\phi_2} f(0, \phi_2)d\phi_2\\&=\int_0^{2\pi}\partial_2gd\phi_2-\int_0^{2\pi}\partial_2g'd\phi_2\\&=\int_0^{2\pi}b(0,\phi_2)d\phi_2-\int_0^{2\pi}b'(0,\phi_2)d\phi_2\\&=\int_2b-\int_2b'\\&=0\text{ (as given) }\end{align*}
Further, since since for all $\phi_1\in[0,2\pi]$, $\partial_1g(\phi_1, 0) = a(\phi_1, 0) = a(\phi_1, 2\pi) = \partial_1g(\phi_1, 2\pi)$ due to continuity of a on $T^2$,
$$\partial_1(g(\phi_1,2\pi)-g(\phi_1,0))=0$$
hence $g(\phi_1,2\pi)-g(\phi_1,0)$ is constant $\forall \phi_1 \in [0,2\pi]$.
Likewise $g'(\phi_1,2\pi)-g'(\phi_1,0)$ is constant over this range. Then their difference
$f(\phi_1,2\pi)-f(\phi_1,0)$ is also constant over $\phi_1\in[0,2\pi]$.
Since $f(0,2\pi)-f(0,0) = 0$, $\forall \phi_1\in[0,2\pi], f(\phi_1,2\pi)-f(\phi_1,0)=0$.
Symmetrically, by making deductions on $\partial_1g$ and $\partial_1g'$, we shall arrive at $$\forall \phi_2\in[0,2\pi], f(2\pi, \phi_2)-f(0, \phi_2)=0.$$
Hence $f$ is $c^\infty$ on $T^2. Thus
$$(a,b) = (a',b') + (\partial_1f, \partial_2f) =(a'b)+df\Rightarrow [(a,b)]=[(a',b')].$$
- Surjective.
For $(r_1, r_2)\in\R^2$ arbitrarily chosen, we shall define closed form $(a,b)=\left(\frac{r_1}{2\pi},\frac{r_2}{2\pi}\right)$ such that $\partial_2a=\partial_1b=0$. Then $(a,b)\in C$ and $[(a,b)] \in \frac{C}{D}, satisfying:
$$H([(a,b)])=\left(\int_0^{2\pi}\frac{r_1}{2\pi}d\phi_1, \int_0^{2\pi}\frac{r_2}{2\pi}d\phi_2\right)=(r_1,r_2).$$
Hence $H$ is an isomorphism that maps between $H^1(T^2,\R)=\frac{C}{D}$ and $\R^2$. Thus the first cohomology group on $T^2$ has dimension 2.
Remarks
I apologize about the notation $(x,y)$ being used interchangeably for a closed form on $T^2$ and a vector on $\R^2$. But one should be able to infer the meanings from the definitions.

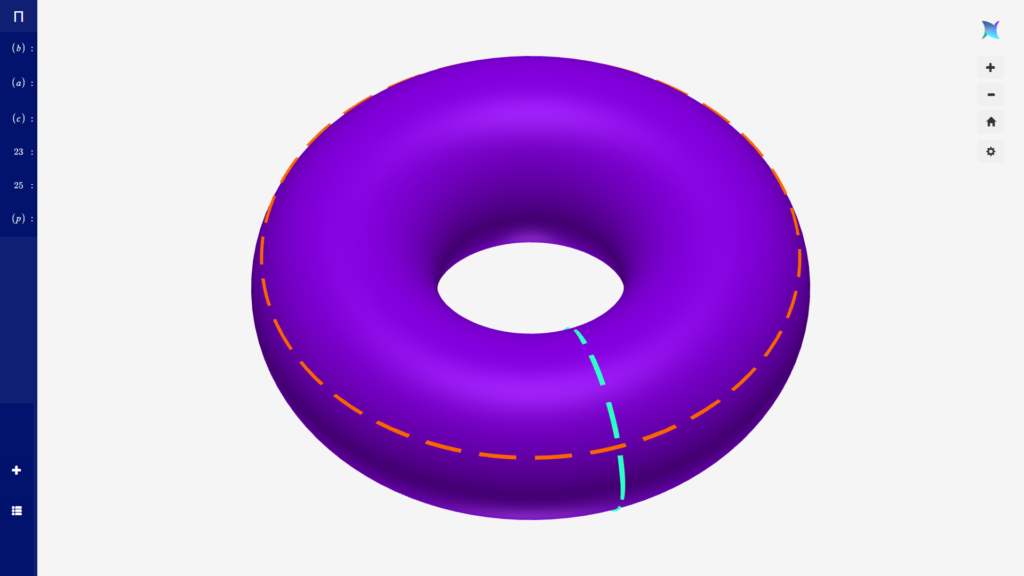
- From the proof of surjection of $H$ as an isomorphism, we see that the two independent dimensions of $\R$ corresponds to the cosets (all the closed forms that are "homologous" to) of the base forms $\omega^1=ad\phi_1+bd\phi_2$, where $a, b\in\R$ are constants from reals. Such $\omega^1$ by itself is closed, because it integrates to 0 over all the boundaries.
- Note that if the lines marked orange and cyan were to be 1-boundaries of some 2-surface, the integral of $\omega^1$ over them will be non-zero. However, these lines are not boundaries to any surfaces due to the particular topology of $T^2$. Hence $ad\phi_1+bd\phi_2$ remains as a closed form over $T^2$, although any "integral" of it will fail to be analytical.
- In fact, integrals over the two marked lines will evaluate to $H(\omega^1)$ as a pair, if they respectively correspond to $\{\phi_2=0\}$ and $\{\phi_1=0\}$. All the closed forms in the coset $[\omega^1]$ will then also evaluate to the same values $H(\omega^1)$ over these two lines, as proven by the "validity" of $H$.