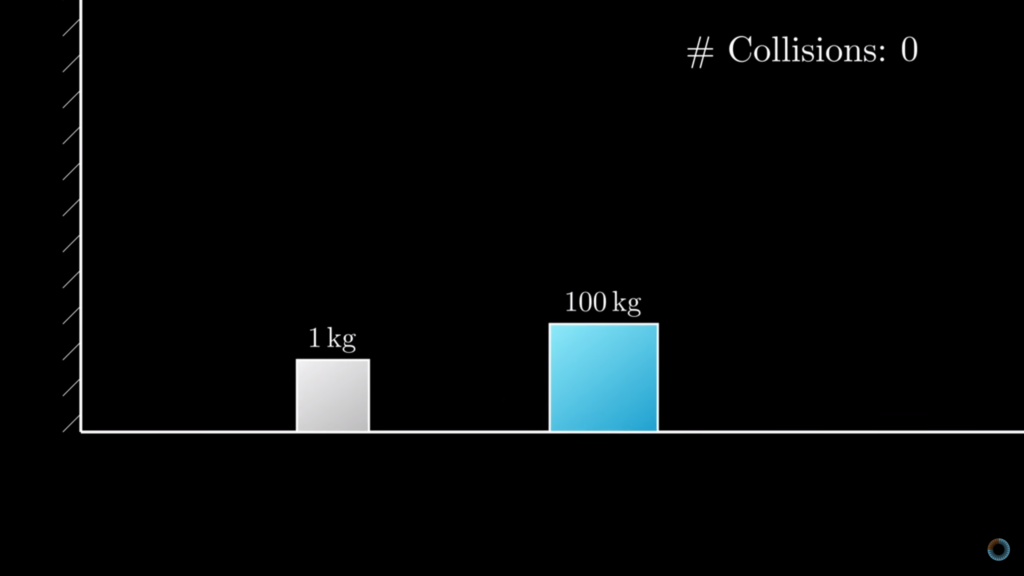
Blue block has mass 1000000, and red block has mass 1; red block initially stationary and blue block moving to the right at 600 pixels per second.
What is the most unexpected way to compute Pi? Imagine you have an elastic wall on the left, a block of mass 1 and a block of mass 100 to its right both on a frictionless rail. The larger block has an initial velocity greater than zero toward the wall. The smaller block toward the left has no initial velocity. If we allow the scenario to proceed, the larger block will slowly move toward the wall, and the smaller block will bounce between the larger block and the wall to transfer momentum, until at a certain point, both blocks start moving to the right and will depart indefinitely. From the descriptions alone one would not see any connections to digits of $\pi$, but if you count the number of collisions that has occurred, both between the wall and the first block, and between the first and the second block, you will get 31.
This is not a coincidence. For a block of mass 1 and a block of mass 1000000, the number of collisions that will occur will be 3141. In general, a block of mass $100^n$ running into a block of mass 1, will result $m$ collisions that correspond to the first $n$ digits of $\pi$. In the video The most unexpected answer to a counting puzzle by 3Blue1Brown, he thoroughly explains the mathematical principles behind this interesting system.
Derek and I wrote a paper to capture the mathematical proof the video back in 2019. We also wanted to create a simulation in Processing, to verify that $\pi$ does indeed show up in collision counts.
Creating the simulation
We begin by creating the block object representing its basic physics properties. We make the block sizes proportional to the log of its mass, so that their visuals can be properly contained in the window.
//Random color arrays generated.
int[][] cols = {{255,0,0},{0,255,0},{0,0,255},{255,255,0},{0,255,255},{255,0,255},
{128,128,0},{0,128,0},{128,0,128},{128,0,0},{215,215,0},{189,183,107},
{143,188,143},{47,79,79},{25,25,112},{218,112,214},{255,235,205},{188,143,143},
{255,218,185},{112,128,144},{230,230,250}};
public class Block implements Comparable<Block>
{
//Horizontal position.
public float x;
//Horizontal velocity.
public float v;
//Mass.
public double m;
//Side length;
public float sideLength;
//Color.
public color col;
//Instantiate a block provided with its mass.
public Block(double m, float x, float v)
{
this.m = m;
this.x = x;
this.v = v;
//Render logrithmically proportional length.
sideLength = (int)Math.log(m);
//Give a color.
//col = color(rand.nextInt(255), rand.nextInt(255), rand.nextInt(255));
if(blockCounter >= blockCount)
blockCounter = 0;
col = color(cols[blockCounter][0], cols[blockCounter][1], cols[blockCounter][2]);
blockCounter++;
}
public int compareTo(Block other)
{
return this.x < other.x? -1: (this.x == other.x? 0: 1);
}
}The Comparable interface naturally orders the blocks based on their $x$ central coordinates. We then create an initializer function that takes an array of parameters specifying the [mass, location, velocity] of each block:
Block blocks[] = new Block[blockcount];
void initBlocks(double[]... inimxvs)
{
for(int i = 0; i < inimxvs.length; i++)
blocks[i] = new Block(inimxvs[i][0], (float)inimxvs[i][1], (float)inimxvs[i][2]);
}We then randomly generate the blocks with masses distributed exponentially between $10^{-10}$ and $10^{10}$.
Visualizing the simulation
We can write the method for each block to visualize themselves:
//Constant vertical surface location of the centers of the blocks.
float surY;
public class Block implements Comparable<Block>
{
//Horizontal position.
public float x;
//Horizontal velocity.
public float v;
//Mass.
public double m;
//Side length;
public float sideLength;
//Color.
public color col;
//...
public void depict()
{
fill(col);
rect(x - sideLength/2, surY - sideLength, sideLength, sideLength);
}
}Now for each draw cycle, we can clear the screen with background(0) and draw the horizontal baseline. Then we visualize the the blocks by calling their depict function.
//Constant vertical surface location of the centers of the blocks.
float surY;
void draw()
{
background(0);
//Draw horizontal rail (baseline)
stroke(255, 255, 255);
line(0, surY, width, surY);
depictBlocks();
}
void depictBlocks()
{
for(Block block: blocks)
block.depict();
}
Computing the simulation
Our initial approach for running the simulation was to update the position of each block during the simulation, and check for collisions in each time frame.
void draw(){
...
//Compute movement.
increment();
//Consider collisions.
//Sort blocks from left to right.
Arrays.sort(blocks);
//Cluster colliding blocks.
boolean onWallPushing = false;
for(int i = 1; i < blocks.length; i++)
{
//Colliding?
if(blocks[i].isColliding(blocks[i - 1]))
{
updatePostCollisionVelocities(blocks[i], blocks[i - 1]);
}
}
//Check for wall-colliders.
if(blocks[0].isPushingWall())
{
// Reverse its velocity if already colliding
blocks[i].v = -blocks[i].v;
}
// Include the following code to turn the right side of the window to a wall as well
// if (blocks[blocks.length-1].x + blocks[blocks.length-1].sideLength / 2 >=width) {
// blocks[blocks.length-1].v = -blocks[blocks.length-1].v;
// }
}
Inside the increment() method, we write logics for updating positions of each block.
void increment()
{
for(int i = 0; i < blocks.length; i++)
blocks[i].x += blocks[i].v/frameRate;
}
Inside a.isColliding(Block b), we write logic for detecting collision between block b and a, by detecting if their boundaries are intersecting. We also write a method to check if the block is bumping into left the wall:
class Block{
//If two blocks are colliding: overlap in volume with co-central distance diminishing.
public boolean isColliding(Block other)
{
Block toTheRight = Math.max(x, other.x) == x? this: other;
Block toTheLeft = toTheRight == this? other: this;
return toTheRight.x - toTheRight.sideLength/2 <= toTheLeft.x + toTheLeft.sideLength/2 &&
(v - other.v)*(x - other.x) < 0;
}
public boolean isPushingWall()
{
return x - sideLength/2 <= 0;
}
}Inside updatePostCollisionVelocities, we write how the block velocities will update based on physical laws:
void updatePostCollisionVelocities(Block a, Block b)
{
float v1 = a.v, v2 = b.v;
double m1 = a.m, m2 = b.m;
a.v = v1+2*(v2-v1)*(float)((m2)/(m1+m2));
b.v = v2+2*(v1-v2)*(float)((m1)/(m1+m2));
}
A problem with the approach
void updatePostCollisionVelocities(Block a, Block b)
{
float v1 = a.v, v2 = b.v;
double m1 = a.m, m2 = b.m;
a.v = v1+(v2-v1)*(float)((m2)/(m1+m2));
b.v = v2+(v1-v2)*(float)((m1)/(m1+m2));
}However, due to the constant framerate of our program, the time intervals taken to compute the block movements is limited to $\Delta t=1.0 sec/100=0.01$. This means if two blocks are close and moving fast, the program will lose track of the dynamics and cause unexpected behaviors (here the right side of the canvas is also turned into a wall to bound the simulation):
Solution 1 --- Adjustable Frame Rate?
One approach to potentially solve the issue is to increase the frame rate whenever a block "over-intesects" another block. This way with higher frame rate the $\Delta t$ between each frames become smaller, resulting in finer simulations --- without slowing it down visually.
To put "over intersection" into precisely measurable conditions, we increase the frame rate whenever there are two collisions detected in two consecutive frames. Logically, two consecutive frames with collisions means that either --- the same pair of colliding blocks was not able to move away from each other in one frame, meaning that their collision was too deep over one frame: $\Delta x = \Delta t \times \Delta v$, or, that the frames are not fine enough to separate two instances of collisions between different pairs.
So we implement the following logic to detect consecutive collisions:
boolean collisionStampA = false;
boolean collisionStampB = false;
float fr = 80;
void draw(){
increment();
// ... visuals
for(int i = 1; i < blocks.length; i++){
//Colliding?
if(blocks[i].isColliding(blocks[i - 1])){
collisionStampA = true;
updatePostCollisionVelocities(new CollisionTuple(blocks[i], blocks[i - 1]));
}
}
// ... collision logics
}
void increment(){
for(int i = 0; i < blocks.length; i++)
blocks[i].x += blocks[i].v/fr;
// Test for consecutive collisions, increase frame rate by 20% if so
if(collisionStampA && collisionStampB){
fr *= 1.2;
frameRate(fr);
}
// otherwise gradually decay framerate until it around 80
else if(frameRate > 80){
fr /= 1.1;
frameRate(fr);
}
collisionStampB = collisionStampA;
}However this solution has some persisting issues:
- When three blocks are running into each other, with two blocks on the sides having much larger mass than the middle one, the middle block will bounce between the two surrounding blocks at high frequencies to transfer a significant amount of momentum much larger than its own. This results in a "squeeze" situation, where the middle block makes $>>100$ collisions per second during the squeeze. Then setting the frame rate to much larger than 100, say 1000 fps, will far exceed the rendering rate of a typical computer, thus slowing down the simulation when $\Delta t = 1.0/fps$ is small.
- If in the above squeeze situation, two blocks have overintersected too much, it is not possible to move them apart over several frames. Then increasing the framerate further reduces the time quanta $\Delta t$, which after a certain point may result in a infinite series of $\Delta x = v_{diff}*\Delta t$ that is never enough to pass the overintersection $$ v_{\text{diff}}\sum_{n=1}^\infty \frac{1}{\text{fps}_0} 1.2^{-n} < \text{ Block A right - Block B left}.$$ In this case the program will fall into an infinite loop and halt.
- The quantization of frames may not match exactly to the theoretical time stamps of collisions. Sometimes this will result in "tunneling", where block A jumps through block B due to reversed ordering, or even moving through multiple blocks due to blown up velocities.
Solution 2 --- Predicting next collision
Now all three of the aforementioned issues can be traced to the common cause of incorrect quantizations of time frames. We can also recognize that the blocks move at constant velocity when not colliding with each other, so their motion can be easily predicted. Thus if we could derive the formula for calculate the time stamp for the next collision, we could quantize the time correctly.
/**
* Gets the time gap between the current time stamp and the next time stamp where the collision will
* precisely occur
*/
float getTimeQuanta(){
// ... To be implemented
}Suppose that we have already figured out how to make the predictions, the next step will be to continuously cache these collisions, and consume these cache during each frame. But this process will create unnecessarily memory overheads if we are caching frames that are finer than the fps displayed. Say there are actually 8000 collisions in a second and the graphics is running at 80 fps, then the states of the system for 100 collisions in between the two frames are actually redundant. In fact, we only need the frames that will be displayed:

If we follow strictly the collision frames, we will be working with the minimal amount of computation, but the time stamps will be misaligned with the rendering engine. For certain periods where there are no collisions over several rendering frames, we would be missing the frames in between causing visual discontinuity. If we follow strictly the rendering frames, then we will need to perform interpolations for each block on screen between the nearest two collision frames. Because the blocks are moving at constant velocities during this period, the interpolation will simply be linear and hence doable --- but still relatively expensive.
The optimal solution should balance the performance and visual continuity by combining the approaches above. That is we quantize to the closest display frame. If the closest collision frame is larger than the display frames of 1/80 second, then we can quantize the collision frames down to 1/80 increments:
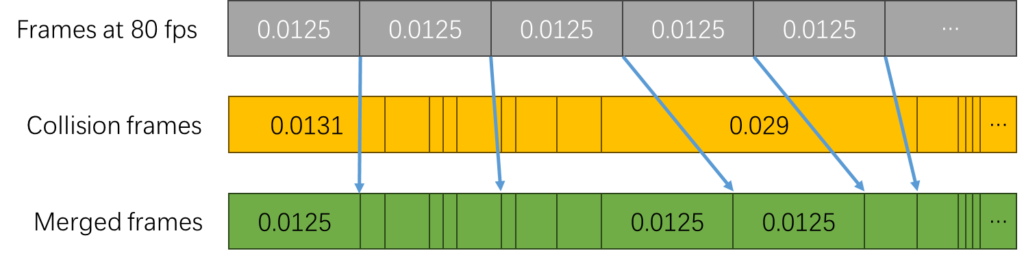
We could also bypass the interpolation with this approach, because offsets of blocks during a single display frame is barely visible to human eyes.
To see how getTimeQuanta() will be implemented, we first realize that collisions will only occur between two neighboring blocks. We know for any of neighboring blocks the time gaps that till their collision: $$\Delta t = \frac{b.leftBound-a.rightBound}{a.v-b.v},$$ assumming they will not collide with any other blocks for this duration (1).
We can also know for sure, that for the next closest collision, it will correspond to the smallest time gap among the set $T = \left\{\frac{b.leftBound-a.rightBound}{a.v-b.v} : (a,b) \text{ neighboring blocks}, a.v>b.v\right\}$, and the assumption (1) is also satisfied for this pair. So getTimeQuanta can be realized by finding the minimum of set $T$.
float getTimeQuanta(){
float timeQuanta = Infinity;
for(int i = 0; i < blocks.length-1; i++){
Block a = blocks[i], b = blocks[i+1];
if(a.v>b.v){
float dt = (b.leftBound()-a.rightBound())/(a.v-b.v);
if(dt<timeQuanta) {
timeQuanta = dt;
}
}
}
return dt;
}To merge the display frames and collision frames will actually be really simple, we just need to set the initial value of $dt$ to 1 over the display frame rate. This way the time quanta to the next frame will be no larger than the quanta between display frames, but can be taken to be much smaller if needed.
float getTimeQuanta(){
float timeQuanta = 1/framerate;
for(int i = 0; i < blocks.length-1; i++){
Block a = blocks[i], b = blocks[i+1];
if(a.v>b.v){
float dt = (b.leftBound()-a.rightBound())/(a.v-b.v);
if(dt<timeQuanta) {
timeQuanta = dt+0.00000001;
}
}
}
return dt;
}In the code above I included a small margin 0.00000001to prevent the collision being undeteced due to floating point error. Next we need to account for the collision between the left most block and the wall. The collision time gap for it can be similarly included:
float getTimeQuanta(){
float timeQuanta = 1/framerate;
// Add special case of collision between left most block and the wall:
if(blocks[0].v<0)
if(blocks[0].leftBound()/-blocks[0].v<timeQuanta)
timeQuanta = blocks[0].leftBound()/-blocks[0].v;
// Add special case of collision between right most block and the wall for bounded simulation:
// if(blocks[blocks.length-1].v>0)
// if((width-blocks[blocks.length-1].rightBound())/blocks[blocks.length-1].v<timeQUanta
// timeQuanta =(width-blocks[blocks.length-1].rightBound())/blocks[blocks.length-1].v;
for(int i = 0; i < blocks.length-1; i++){
Block a = blocks[i], b = blocks[i+1];
if(a.v>b.v){
float dt = (b.leftBound()-a.rightBound())/(a.v-b.v);
if(dt<timeQuanta) {
// To prevent time quanta from being too small to trigger collisions
timeQuanta = dt+0.00000001;
}
}
}
return dt;
}Next we just need to incorporate this routine into the draw() loop. Previously draw() calls increment() and computes collisions. Now we can abstract these methods into a new method called getFrame(float timeStamp), where timeStamp is the time of the rendering where draw() is called. We keep track of the rendering time with timeStamp, and the simulation time with t. The role of $getFrame$ is to run the simulation up to the next time stamp beyond the rendering timeStamp, over any necessary iterations of quantas of collisions:
float timeStamp = 0;
void draw()
{
background(0);
//Draw horizontal boundary.
stroke(255, 255, 255);
line(0, surY, width, surY);
//Increment to new time stamp
timeStamp += 1/frameRate;
//Compute movement up to timeStamp
getFrame(timeStamp);
//Implemented as above
depictBlocks(frame);
}
float t = 0;
void getFrame(float timeStamp)
{
//Consider collisions.
//Sort blocks from left to right.
while(t<timeStamp){
computeCollisions();
increment();
}
}Inside increment(), we move the blocks to their positions at the next quanta. We also increment the global variable $t$. Notice that we don't need to pass the positions of blocks around explicitly, as the static global field blocks is modified over each iterations:
void computeCollisions(){
//Check for wall-pushers.
if(blocks[0].isPushingWall())
{
blocks[0].v = -blocks[0].v;
collisionCount++;
}
// Right wall
// if (blocks[blocks.length-1].x + blocks[blocks.length-1].sideLength / 2 >=width) {
// blocks[blocks.length-1].v = -blocks[blocks.length-1].v;
// collisionCount++;
// }
for(int i = 1; i < blocks.length; i++)
{
//Colliding? perform elastic collision computation
if(blocks[i].isColliding(blocks[i - 1]))
{
updatePostCollisionVelocities(blocks[i], blocks[i - 1]);
collisionCount++;
}
}
}
void increment()
{
float dt = getTimeQuanta();
t+=dt;
for(int i = 0; i < blocks.length; i++)
blocks[i].x += blocks[i].v*dt;
}We set the global frame rate to 80. The combined result is as followed.
Optimizing the simulation
Now by predicting the next collision, we have solved the issue of instability in simulations. There are two minor points that could be improved however. One is that the time quanta is given a 0.00000001 margin to prevent the collision being left undetected due to floating point error. A small number yet still a source of inaccuracies and instability when collision frequencies reach up to $10^8$ Hz. The second problem is that the displayed frames are actually aligned to the next closest quanta, instead of being precisely aligned to rendering time stamps. This will cause a very slight shaking to the gliding motion of blocks. We fix these errors by:
- Recording the index of the block pair contributing to the minimal quanta to the next collision; if no collision till the next time stamp, index will be -1. computeCollisions collides the blocks at this index directly, instead of attempting to detect by position inequalities.
- Pass to getTimeQuanta the gap till the next rendering frame as the initial value of time quanta, this way if there are no collisions between now and the next frame, the time will jump directly to the next frame instead of somewhere beyond it.
- We set the terminal criterion for the while loop in getFrame to have a margin of 0.00000001, to avoid floating point errors that keeps the while loop running. This will not impact computation accuracy.
float t = 0;
void getFrame(float timeStamp)
{
//Consider collisions.
//Sort blocks from left to right.
while(t<timeStamp-0.00000001){
step(timeStamp-t);
}
}
void step(float timeGap)
{
float timeQuanta = timeGap;
int index = -1;
// Add special case of collision between left most block and the wall:
if(blocks[0].v<0)
if(blocks[0].leftBound()/-blocks[0].v<timeQuanta){
timeQuanta = blocks[0].leftBound()/-blocks[0].v;
index = 0;
}
// Add special case of collision between right most block and the wall for bounded simulation:
// if(blocks[blocks.length-1].v>0)
// if((width-blocks[blocks.length-1].rightBound())/blocks[blocks.length-1].v<timeQUanta){
// timeQuanta =(width-blocks[blocks.length-1].rightBound())/blocks[blocks.length-1].v;
// index = blocks.length;
// }
for(int i = 0; i < blocks.length-1; i++){
Block a = blocks[i], b = blocks[i+1];
if(a.v>b.v){
float dt = (b.leftBound()-a.rightBound())/(a.v-b.v);
if(dt<timeQuanta) {
// To prevent time quanta from being too small to trigger collisions
timeQuanta = dt;
index = i+1;
}
}
}
increment(timeQuanta);
computeCollisions(index);
}
void increment(float timeQuanta){
t+=timeQuanta;
for(int i = 0; i < blocks.length; i++)
blocks[i].x += blocks[i].v*timeQuanta;
}
void computeCollisions(int index){
//Check for wall-pushers.
if(index == 0)
{
blocks[0].v = -blocks[0].v;
collisionCount++;
}
// Right wall
// else if (index == blocks.length) {
// blocks[blocks.length-1].v = -blocks[blocks.length-1].v;
// collisionCount++;
// }
else if(index>0)
{
updatePostCollisionVelocities(blocks[index-1], blocks[index]);
collisionCount++;
}
}